Sul lato SUD del campanile di Giotto a Firenze c'è una formella famosa; tale immagine è infatti utilizzata in molti libri di astronomia. Ma cosa rappresenta? Si tratta di un astronomo, per la precisione Tolomeo, intento ad osservare gli astri mediante uno strumento: il quadrante o quadrante di altezza che è proprio quello che costruiremo ed impareremo ad usare.

A cosa serve? Serve a misurare l'altezza di un astro, o di un oggetto, dalla linea dell'orizzonte. Un oggetto che si trova all'orizzonte ha una altezza di 0° mentre un oggetto posizionato sopra la nostra testa (Zenit) ha una altezza di 90°. (vedi la pagina del'astronomo dilettante dedicata alle coordinate altazimutali).

La realizzazione è molto facile utilizzando il disegno riportato qui accanto che puoi scaricare anche in formato PDF.
 

In realtà ho realizzato 12 disegni diversi e precisamente uno per ciascuna delle latitudini comprese tra 36° e 47°.

Per scegliere il disegno che fa per te basta fare click in corrispondenza  del luogo che ti interessa e scaricherai così  direttamente la versione PDF del disegno corrispondente a quella latitudine.

Inglese

LONGITUDINE

Qui accanto trovi la solita cartina ma con un click la potrai scaricare in alta risoluzione; dovrebbe permetterti di conoscere approssimativamente le coordinate del posto dove sei. Per i nostri fini l'approssimazione è più che sufficiente.

Realizzazione.

Allora, stampa il disegno che hai scaricato su un cartoncino di formato A4.

Procurati un supporto in masonite o compensato delle dimensioni adeguate al disegno (circa 20x20cm) e dello spessore di almeno 4 mm; io ho utilizzato il retro di una cornice a giorno delle dimensioni di 20x30 cm al quale ho tagliato via un pezzo.

Nel lato posteriore applica una maniglia di quelle da cassetti e fissala con le viti a testa svasata. Le viti saranno ovviamente sul lato anteriore e pertanto non devono fuoriuscire dal piano.

Incolla il disegno sul lato anteriore del supporto (ma non usare colle ad acqua come il Vinavil poiché rischieresti di far imbarcare il tuo quadrante).

Se vuoi proteggere il disegno puoi verniciare il disegno con una vernice a spruzzo trasparente (non all'acqua). Prima però fai una prova su un campione in modo da verificare che la vernice non sciolga il colore.

Provvedi a fare un foro piccolo (1 mm o anche meno) in corrispondenza del punto A ed un foro da 3 mm in corrispondenza del punto B.
 

Applica in B una vite M3x20 o M3x30 (meglio se di ottone) in modo che fuoriuscendo possa servire a fare l'ombra del sole. Per il fissaggio utilizza anche due rondelle in modo da garantire la perpendicolarità della vite rispetto alla superficie del quadrante.

In A invece passa del filo di nylon da pesca da 0,3 mm, appesantito in fondo con un piombo da 20 g (o da 10 g) ed a distanza di 22 cm fissa un altro piombino N. 5 (la scatola diceva che il peso era da 0.132 g e 2.9 mm di diametro). Il piombo grande serve a tendere il filo in verticale mentre quello piccolo va regolato sul periodo dell'anno e svolge la funzione di indice.

Sul lato posteriore ho creato una frizione per il filo di nylon in modo da rendere particolarmente agevole la regolazione del filo stesso. Ho utilizzato un feltrino al quale ho praticato un taglio attraverso il quale ho fatto passare il filo; sopra questo feltrino ne ho messo un altro sempre col taglio ma incollato ortogonalmente al primo. Se l'azione frenante non fosse sufficiente è sempre possibile aggiungere un altro feltrino.

Per evitare che il filo possa sfuggire è stato legato ad un bottone per mezzo del nodo di bulin.

Come ultima cosa occorre fare una protezione alla vite; la protezione non serve per la vite stessa che è fin troppo robusta ma per il contenitore che ospiterà il quadrante e che potrebbe anche forarsi in corrispondenza della vite.
La protezione che ho realizzato è un sughero di altezza tale da contenere la vite e nel quale ho praticato un foro da 2,4mm.

Inglese

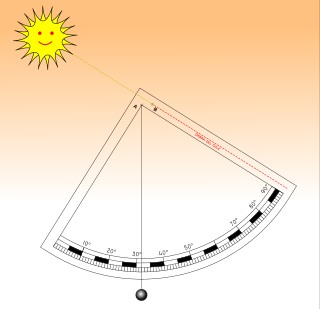Qui accanto è illustrato l'uso base del quadrante di altezza; posizioniamolo in modo che l'ombra del sole sia lungo la scritta "ombra del sole"; l'altezza del sole sull'orizzonte si legge sulla scala graduata sotto il filo a piombo.

Nell'esempio la lettura è pari a 32°.

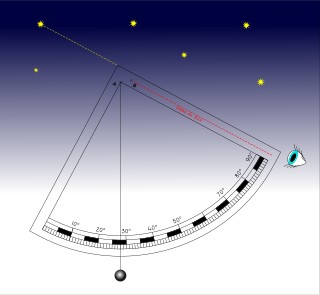Se invece vogliamo misurare l'altezza di un astro occorre allineare lo stesso col bordo superiore del quadrante mirandolo come nel disegno accanto. La lettura si esegue come sopra.

Attenzione: non usare mai questo metodo per misurare l'altezza del sole.

Inglese

Qui di seguito c'è la scala dei mesi; la scala è ciclica nel senso che per percorrere l'anno completamente occorre scorrerla in modo ciclico. Leggiamo quindi giugno, luglio, ..., novembre, dicembre. Per continuare dobbiamo procedere in basso ma da destra verso sinistra. Leggiamo quindi dicembre, gennaio, ..., maggio, giugno.

Inglese

Le estremità della scala rappresentano il solstizio d'estate (sinistra) e il solstizio d'inverno (destra); dal punto di vista grafico si può notare come sono stati disegnati all'incirca intorno al 20 di giugno e al 20 di Dicembre.

Inglese

Ora vediamo come utilizzare il quadrante di altezza per conoscere l'ora. Dobbiamo ovviamente conoscere la data.

Nell'esempio mostrato accanto la data è quella del 10 di agosto (la valutazione ovviamente è approssimativa). Per semplificare la lettura dovremo far scorrere il filo a piombo in modo che il piombino piccolo si porti all'altezza corrispondente alla data prescelta. L'ora si leggerà sulla linea curva rossa. Nell'esempio accanto potremo stimare le ore 7:45 del mattino oppure le ore 16:15 del pomeriggio. Poiché c'è l'ora legale occorre aggiungere un'ora e pertanto abbiamo le 8:45 (oppure le 17:15)

(Per inciso faccio notare che questa lettura era la stessa anche per il 1° maggio)

Lo stesso angolo per l'altezza del sole letto il 20 settembre (o 20 marzo) corrisponde alle ore 8:50 mentre il 1° marzo (o 10 ottobre) corrisponderebbe alle 9:40.

Le ore indicate sono ore solari; quando c'è l'ora legale occorre aumentare di un'ora il valore indicato.

(nota: i grafici del quadrante accanto sono stati costruiti prendendo a riferimento la latitudine di 44°)

Come conferma ho verificato con un programma planetario che qui a Firenze (44° di latitudine e 11° di longitudine) il 10 agosto l'altezza del sole era pari a 30° alle ore 8:09 solari (e quindi 9:09 ora legale).

Inglese

L'errore che commettiamo utilizzando questo strumento deriva dall'accuratezza con cui sono state disegnate le curve, dalla precisione con cui misuriamo l'altezza del sole e da altri due fattori che però siamo in gradi di compensare.

Il primo di questi fattori consiste nel fatto che il meridiano di riferimento per l'Italia si trova ad una longitudine di 15° (corrispondenti ad un'ora che è quella che ci separa dal meridiano di Greenwich) Ma noi siano ad una latitudine di 11°, cioè il sole è in ritardo di 4 gradi rispetto al nostro riferimento. Ma se 15° corrispondono ad 1 ora, 1 grado corrisponde a 4 minuti (60/15) e quindi 4 gradi corrispondono a 16 minuti (4x4). In sostanza, per compensare il fatto che ci troviamo ad una longitudine di 11° dobbiamo sommare 16 minuti alla nostra lettura.

Per semplificare il calcolo, sul quadrante è riportata la scala seguente:

LONGITUDINE

CORREZIONE IN MINUTI

Quindi in alto leggiamo la longitudine ed in basso i minuti di correzione corrispondenti.

Il secondo di questi fattori va ricercato nell'inclinazione dell'eclittica e nell'eccentricità dell'orbita. La somma di questi due fattori è conosciuta col nome EQUAZIONE DEL TEMPO ed è rappresentata dal grafico seguente:

I valori variano da un massimo di circa 14 minuti ad un minimo di -16 minuti circa. In corrispondenza del 10 di agosto stimiamo una correzione pari a 5 minuti che vanno ad aggiungersi ai precedenti.

Riassumendo la compensazione totale è pari a 16+5=21 minuti che andranno a sommarsi alla nostra lettura; pertanto l'ora stimata e compensata è pari a 7:45 + 0:21 e cioè 8:06

Forse siamo stati fortunati ma il risultato mi sembra ottimo.

Costruisci il quadrante e fai da te le verifiche.

Qui puoi scaricare il file che riassume quanto spiegato sopra; potrai stamparlo e portarlo con te insieme al quadrante di altezza.

Inglese

Come ultima informazione sul nostro quadrante di altezza è riportata la scala delle tangenti; questa scala ci permette di calcolare la distanza se conosciamo l'altezza dell'oggetto che vediamo o viceversa calcolare l'altezza se ne conosciamo la distanza.

Inglese

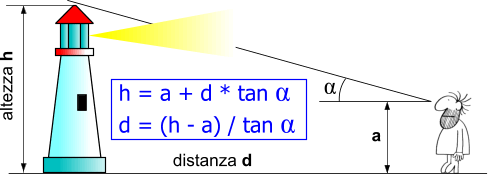
Supponiamo di vedere un palazzo di 15 piani (stimiamo un piano pari a 3 m per cui h=15x3=45m). Misuriamo l'altezza α (ad esempio 30°) e leggiamo sulla scala blu la tangente di α (tan α = 0,58); inoltre stimiamo a=1,6m (altezza dei nostri occhi da terra). Utilizzando la formula precede otteniamo d=(45-1.6)/0,58=74,8m.

La formula può essere utilizzata anche a rovescio e cioè ci permette di determinare h se conosciamo la distanza d.

Inglese

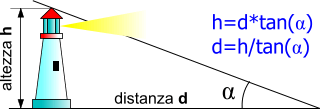Nel caso in cui l'altezza h è particolarmente rilevante rispetto alla nostra altezza, possiamo trascurare quest'ultima ed in questo caso le formule da utilizzare sono quelle a lato.

Voglio qui ringraziare il prof. Franco Martinelli al quale questo mio quadrante si è ispirato. Al seguente indirizzo

http://www.nauticoartiglio.lu.it/almanacco/quaderni/www/quadrante/WITN_quadrante.htm

trovi il suo lavoro ed anche interessanti aspetti storici.

Il mio lavoro differisce da quello nei seguenti punti:

Ho provveduto a ricalcolare le curve ed ho utilizzato una scala dei mesi di tipo lineare (più semplice da leggere) invece di una scala lineare per le declinazioni del sole (più difficile da leggere); questo è il motivo per cui le curve hanno forma diversa.

Ho realizzato 12 disegni diversi (nelle latitudini comprese tra 36° e 47°) in luogo di una sola a 45° al fine di aumentare la precisione nella lettura dell'ora.

I disegni forniti sono dei PDF vettoriali e quindi forniscono stampe di elevata qualità anche di dimensioni maggiori (ovviamente diminuisce la portabilità ma aumenta - forse - l'accuratezza)

Ho introdotto sul quadrante (col solo scopo di promemoria) l'equazione del tempo e la correzione della longitudine.

Nella formula del calcolo di distanza in funzione dell'altezza (e viceversa) ho introdotto l'altezza dell'osservatore; ciò è stato fatto poiché mio figlio Filippo ha provato ad usarlo per misurare l'altezza di un oggetto basso (un palo di circa 2 metri) ed in quel caso l'errore era intollerabile.

Inglese