Di cosa parliamo questa volta?
 

What are we speaking about?

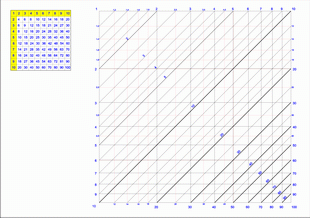
La tabellina, quella pitagorica, la conosciamo tutti dai tempi delle elementari e ci è molto utile per fare le moltiplicazioni ed anche le divisioni.

Quella che vi presento ora è invece la tabella grafica inventata da Pouchet-Lalanne e permette di fare moltiplicazioni anche tra due numeri non interi; il prezzo che si paga è la precisione che è inferiore al calcolo fatto utilizzando carta e matita a vantaggio di una risposta quasi immediata.

Vediamo come funziona. (Per seguire meglio gli esempi conviene stampare il grafico in alta risoluzione o )

Probably since the primary school you learned the use of Pitagoric Table, to make multiplication and divisions.

But now I show you a table, created by Pouchet-Lalanne, that allow to multiply numbers also if they are non integers. The table gives results very fast but the accuracy of calculation is lower in comparison with handmade calculation.

Let’s see how it works. (To view the table better, you should print it in high resolution or ).

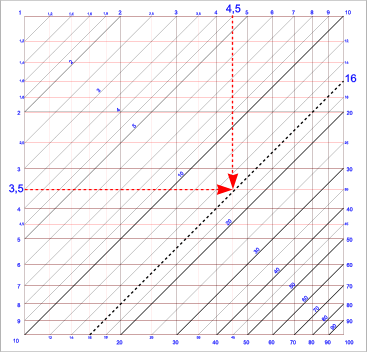Supponiamo di voler moltiplicare 3,5 x 4,5

E' sufficiente cercare l'intersezione dei due valori e leggere il risultato sulla retta inclinata a 45° vicino a questa intersezione; nel caso specifico la retta è quella di valore 16 e il nostro occhio vede che si tratta di un valore un po' inferiore a 16; potremmo valutare il risultato in circa 15,5.

Facendo il calcolo troviamo che 3,5x4,5=15,75 e non 15,5 ma in questo caso abbiamo fatto un errore inferiore al 2%.

Let’s suppose to multiply 3.5 and 4.5.

You should locate the intersection of those two values, and then read the result on the nearest inclined line. In our case the line is the one with value 16, and we can appreciate that the value is a little less than 16, about 15.5.

If we do a manual calculation we find 3.5x4.5=15.75, that’s more than 15.5 and you see that we had an error less than of 2%.

Se i due fattori non sono compresi tra 1 e 10 occorre dapprima ridurre il prodotto a due fattori entro questi limiti e ricordarci poi di mettere la virgola nel posto giusto. (lo stesso di quello che si fa utilizzando il regolo o il nomogramma dei prodotti)
 

If the two factors are not included between 1 and 10, first you need to reduce them such to remain inside those values, and then add the comma to the result, in the right place (it’s the same process when we multiply using the slide rule or the nomogram.
 

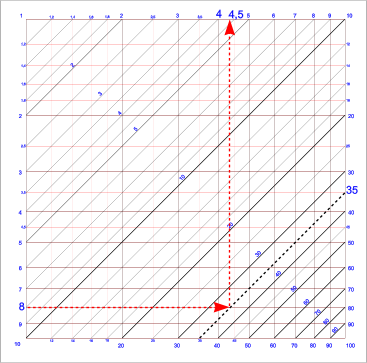E' possibile fare anche le divisioni partendo dalla linea inclinata, incrociando il divisore sulla retta orizzontale e trovando il risultato con la retta verticale che passa per l'incrocio.

Ad esempio supponiamo di voler fare 35/8.

Portiamoci sulla linea inclinata di valore 35 e cerchiamo l'incrocio con la retta orizzontale di valore 8; questo punto è vicino alla retta verticale 4,5 ma noi la approssimeremo ad occhio ad un valore pari a 4,3. Il valore vero calcolato è 4,375 ed anche in questo caso l'errore è inferiore al 2%.

You can also divide two numbers, starting from the point where the horizontal line of the divisor cross the inclined line, finding the result on the corresponding vertical line.

Let’s suppose to do 35:8.

On the inclined line we search for the intersection with the horizontal line of value 8. This point is near to the vertical line corresponding to 4.5. >

Per la lettura delle scale logaritmiche puoi andare qui.

Go here if you need help to read logarithmic scale